Fraktalne wzory w przyrodzie

Od struktury ludzkich płuc, poprzez kształty muszli aż do galaktyk – w przyrodzie nie ma przypadków. Fraktale mimo iż składają się z chaotycznych elementów, zawierają swoje własne wzory wzrostu.
Matematyczne piękno fraktali polega na niekończącej się złożoności stworzonej ze stosunkowo prostych wzorów. Oto lista naturalnych przyrodniczych fraktali.
Brokuły
Ten naturalny wzór jest najlepszym przykładem na fraktale występujące w przyrodzie. Wzór wzrostu brokułu jest naturalną reprezentacją złotego podziału – ciągu Fibonacciego, spirali logarytmicznej, gdzie każde ćwierć obrotu jest oddalone od początku o współczynnik liczby pi.


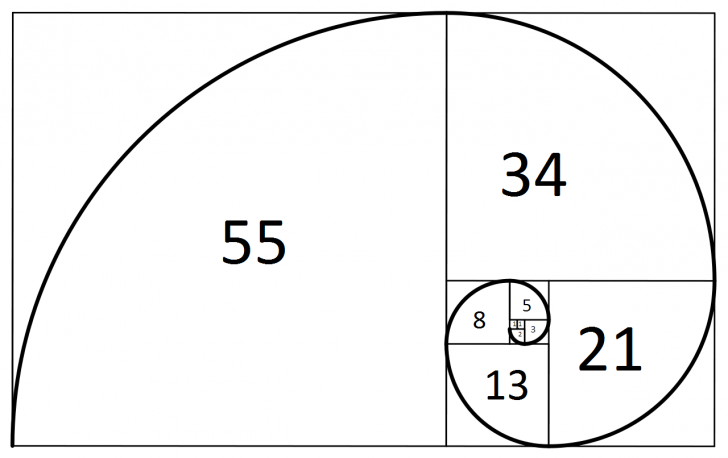
Reprezentacja graficzna ciągu Fibonacciego
Solanki
Zdjęcie poniżej to zatoka San Francisco, gdzie od kilku stuleci pozyskuje się sól na potrzeby komercyjnego rynku. Wytracająca się w wody sól tworzy inkrustacje, które choć przypadkowe mimo wszystko tworzą niezwykle spójny wzór, charakterystyczny dla fraktali.

Amonity
Wymarłe 65 tysięcy lat temu amonity były morskimi głowonogami, które budowały spiralne, komorowe muszle. Ściany między poszczególnymi komorami zwane szwami były fraktalnie ułożonymi krzywymi.

Niektórzy naukowcy odwołują się do przykładu amonitów, wskazując, że w przyrodzie nie występuje rozwój w kierunku większej złożoności. Muszle amonitów przyrastają w kształcie spirali logarytmicznej – wzoru, który bardzo często pojawia się w przyrodzie.
Struktura amonitów inspirowała niejednokrotnie architektów, np. podczas budowy schodów w katedrze w Barcelonie.


Góry
Pasma górskie są wynikiem pracy sił tektonicznych pchających ku sobie powłoki skorupy ziemskiej, powodując ich wypiętrzenie oraz erozję, która redukuje część z powstających elementów. Efektem jest fraktalny wzór.
Zdjęcie przedstawia Himalaje – w tym górskim paśmie znajdują się najwyższe szczyty istniejące na ziemi. Himalaje wciąż się wypiętrzają w wyniku ciągle pracującej kolizji półwyspu indyjskiego z kontynentem euroazjatyckim, która rozpoczęła się 70 milionów lat temu.

Paprocie
Są popularnym przykładem matematycznej właściwości samopodobieństwa zbioru, co oznacza, że jego struktura może być matematycznie generowana i odtwarzana w dowolnym powiększeniu lub pomniejszeniu. Wzór matematyczny, opisujący fraktalny układ paproci, nazwany został od imienia jego popularyzatora Paprocią Barnsleya.
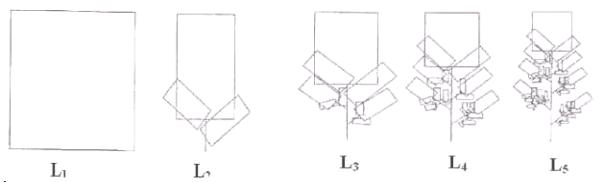
Wzór pokazuje, że chaos będący z natury nieprzewidywalny podażą za deterministycznymi regułami, opierającymi się na nieliniowych równaniach interaktywnych. Mówiąc inaczej – że przypadkowe liczby generowane w kółko, zgodnie ze wzorem paproci Barnsleya, finalnie utworzą uporządkowany fraktalny obiekt.


Chmury
Chmury typu stratus zostały sfotografowane przez satelitę Aqua nad południowym Atlantykiem, na zachodnim wybrzeżu Afryki. Fraktalny wzór chmur został zakłócony przez szereg ukośnych rowów. Zdaniem naukowców z NASA jest to niezwykle rzadkie, aby w zwartej strukturze stratusów zobaczyć tak wyraźną granicę w nieustannie tworzących się chmurach.


Liście
Wiele liści odtwarza proste cykle w tworzeniu swoich rozgałęzień i wzorów. Co ciekawe postępująca deforestacja przebiega również w podobnym wzorze.



Kaniony rzek
To sztucznie barwione zdjęcie przedstawia fraktalny wzór Wielkiego Kanionu, wydrążonego przez rzekę Kolorado w ciągu milionów lat. Kolor czerwony wskazuje obszary roślinności na obrazie.

Błyskawice
Linia błyskawicy powstaje stopniowo w miarę, gdy energia zbliża się krok po kroku w kierunku ziemi, zamieniając okoliczne powietrze w elektryczną plazmę jonów i elektronów.

Paw
Samiec tego ptaka przyciąga samice powtarzającym się wzorem upierzenia na swoim imponującym ogonie.


Płatki śniegu
Skrystalizowana woda tworzy powtarzający się w płatkach śniegu i na zamrożonych powierzchniach wzór. Jest to jeden z pierwszych opisanych fraktalnych wzorów – krzywa Kocha. Została ona opisana po raz pierwszy w roku 1904 przez szwedzkiego matematyka Helgego von Kocha.
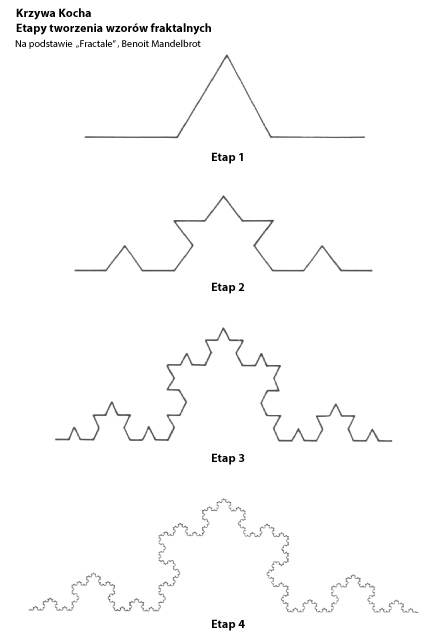
Krzywa Kocha powstaje z odcinka, poprzez podzielenie go na 3 części i zastąpienie środkowej ząbkiem (o ramieniu długości równej 1/3 odcinka) takim, że wraz z usuwaną częścią tworzy trójkąt równoboczny. Krok ten jest powtarzany w nieskończoność, dla każdego fragmentu odcinka.
Jest ona nieskończenie długa, mieści się jednak na skończonej powierzchni – można więc narysować pewne jej przybliżenie. [via]

Zdjęcie Alexey Kljatov

Zdjęcie Alexey Kljatov

Zdjęcie Alexey Kljatov
Wodospady
Podobnie jak w przypadku kanionów krzywizny skał i siła grawitacji, powodująca spływanie wody w dół, przyczynia się do powstania powtarzającego się wzoru.

Delty rzek
Przykładem niech będzie rzeka Jukon, którą widzimy na zdjęciu. Rozgałęzia się ona na tysiące kanałów dostarczających wodę do Morza Beringa na wybrzeżu Alaski.
Rzeka podąża w kierunku od prawej do lewej strony, morze widoczne jest w lewym górnym rogu zdjęcia.

I jeszcze jeden spektakularny przykład:

Doñana National Park, Andaluzja, Hiszpania. Zdjęcie Hector Garrido
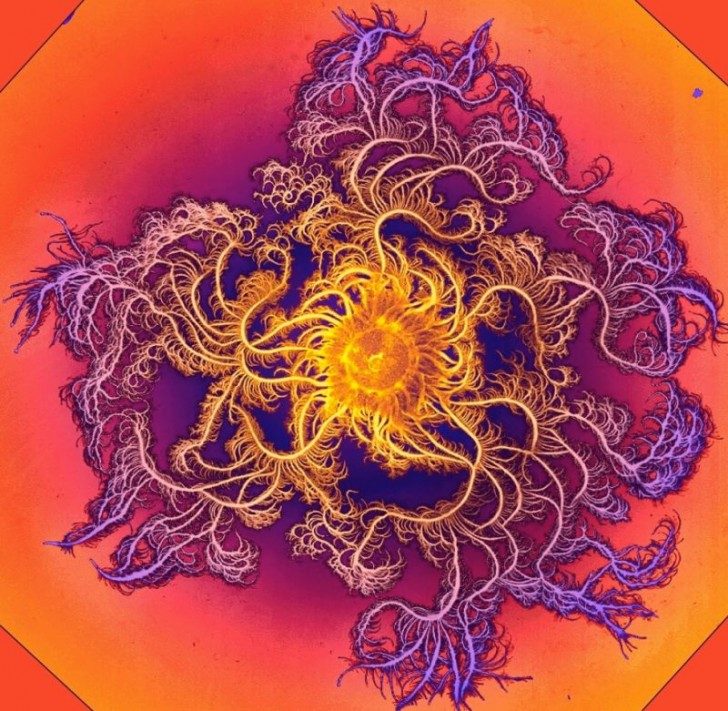
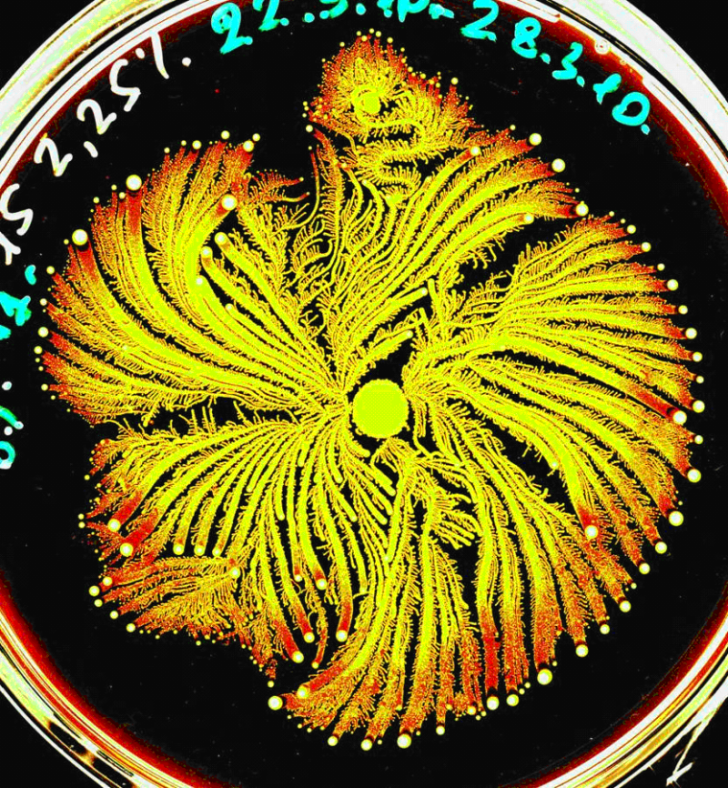
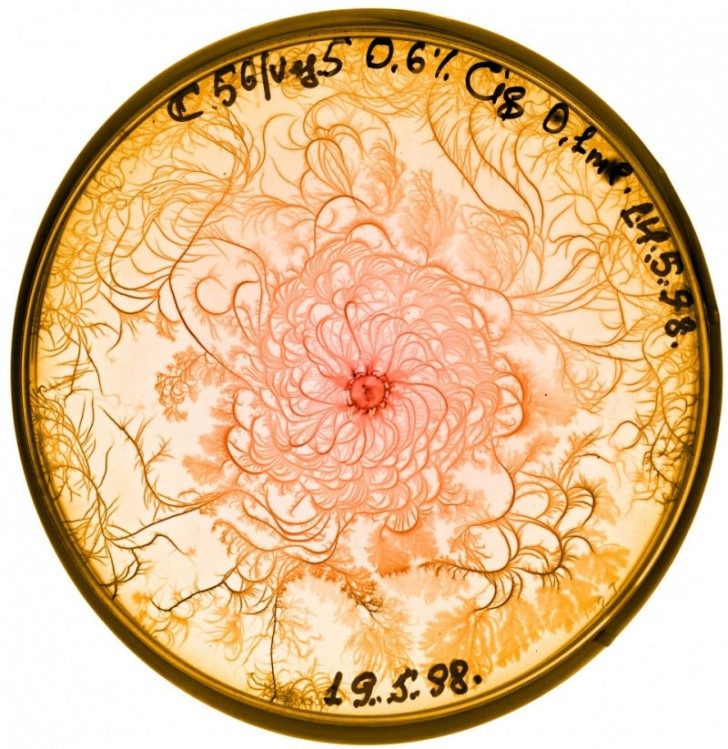
Bakterie tworzące fraktalne wzory na szalce Petriego
Badania wykazały, że bakterie rozwijają się w jednym kierunku, ale gdy duża liczba rozrastających się komórek napiera na siebie, dochodzi do zakłóceń. Komórki dzieląc się dalej, powielają schemat, co prowadzi do powstawania samopodobnych wzorów, czyli fraktali.