Geometria roślin. Ciąg Fibonacciego w przyrodzie
Tak manifestują się podstawowe prawa matematyki w przyrodzie.

Ciąg Fibonacciego jest nie tylko teoretycznym założeniem matematycznym – urzeczywistnia się również niezwykle często w przyrodzie.
Spiralny kształt, w którym każdy element jest sumą dwóch poprzednich identycznych elementów, zaobserwował i wyliczył w XII wieku włoski matematyk, od którego nazwiska bierze swoją nazwę ciąg Fibonacciego.
Złoty podział, nazywany również złotą proporcją, wyznacza odcinek, w którym większa część pozostaje w takiej samej relacji do mniejszej, jak całość do większej.
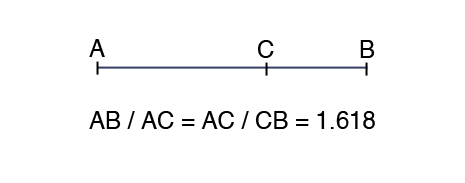
Z ciągiem Fibonacciego wiąże się również niezwykła zależność: dzieląc dowolną liczbę ciągu przez liczbę ją poprzedzającą otrzymamy wynik oscylujący wokół 1,61804 – liczby zapisywanej w greckim alfabecie jako Φ – (fi). Platon uważał, że liczba ta może być kluczem do Wszechświata, a w starożytnych pismach często uważana jest ona nie tylko za Złotą lecz również Boską Liczbą, pozwalającą na uporządkowanie chaotycznego wszechświata.
Ta banalna z pozoru zależność w rzeczywistości opisuje cały szereg zjawisk występujących w przyrodzie, począwszy od roślin aż po kształt galaktyk.
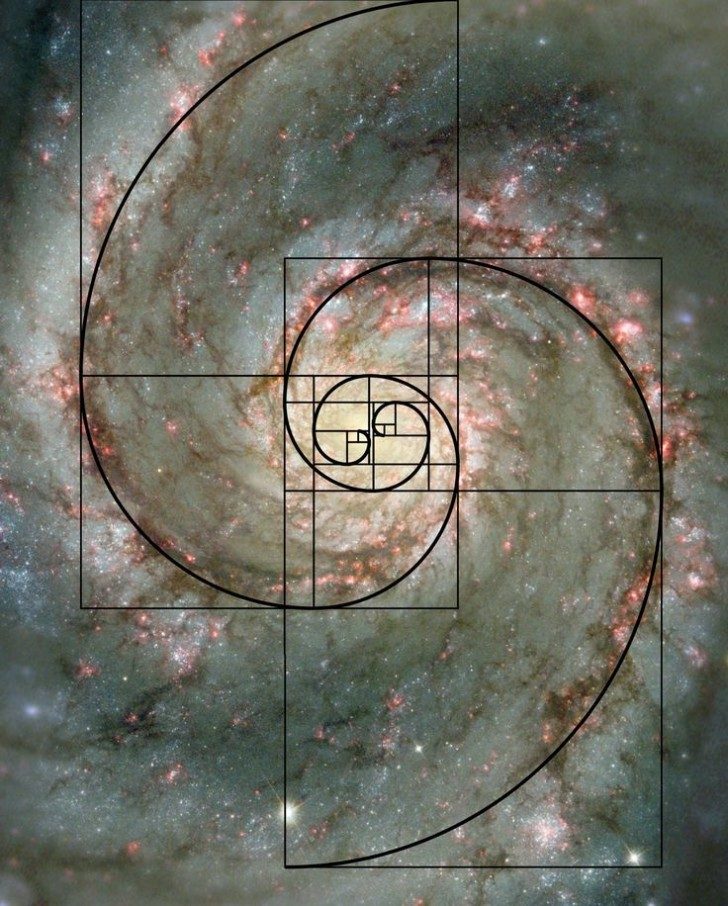

W kształtach wielu roślin widać spiralne linie rozchodzące się od środka w niezwykle usystematyzowany sposób. Rośliny rozwijając się wypuszczają kolejne pędy z jednego centralnego punktu (np. łodygi) rozchodząc się pod kątem. Kąt ten to w przybliżeniu ok. 13,5 stopnia w stosunku do wcześniejszego zawiązka.

Zestawienie pokazuje jak wygląda rozmieszczenie nasion według Złotego Podziału (C) oraz jak wyglądałoby, gdyby natura wybrała inną liczbę (A i B).
Jest to tak zwany Złoty Kąt, który wyznacza kierunek rozwoju roślin. Jak się okazuje on również zawiera w sobie ciąg Fibonacciego – jest to złota proporcja dla podziału okręgu.
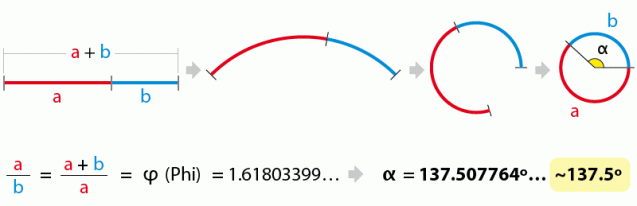
Kiedy pojawiają się kolejne zawiązki, każdy następny utworzy z poprzednim właśnie „złoty kąt”. Dzięki temu nie będą one wyrastać z łodygi promieniście, lecz właśnie spiralne.













Złota proporcja znalazła również swoje zastosowane w świecie sztuki. Dzieła stworzone w oparciu właśnie o tę zasadę wydają się nam w odbiorze niezwykle atrakcyjne.

Mona Lisa, Leonardo da Vinci, 1503–1506.

Święta Anna Samotrzecia, Dziewica z Dzieciątkiem i Św. Anną, Leonardo da Vinci, 1506-1513.