Matematyka stojąca za hipnotycznymi niepowtarzającymi się wzorami
Od kostki brukowej poprzez marokańskie mozaiki aż do pszczelego ulu – występujące w przyrodzie i popularne w architekturze mozaiki kryją w sobie interesujące matematyczne zależności.

Układy składające się z dużej ilości identycznych obiektów, tworzących zwartą powierzchnię bez nachodzenia na siebie i szczelin pomiędzy poszczególnymi elementami, są w matematyce określane tesselajcą.
Jeśli przesunęlibyśmy całą mozaikę o jeden element do góry, albo przekręcili każdy tworzący ją kafelek o 90 stopni, uzyskalibyśmy dokładnie ten sam wzór. To dlatego, że cała mozaika ma taką samą symetrię jak każdy pojedynczy element ją tworzący.
Parkietaż periodyczny
Przykładem najprostszego parkietaża jest mozaika składająca się z kwadratowych płytek, będąca odzwierciedleniem kształtu i symetrii jej części składowych. Układ taki łatwo przesunąć (dokonać translacji) o dowolny wektor nie wywołując zmiany wzoru. Tego rodzaju parkietaż określamy mianem periodycznego. Zapewne wielu z was ma przykład takiego układu w swojej łazience czy kuchni.

Co ciekawe spośród wszystkich możliwych aranżacji, to właśnie te regularne układy są preferowane przez naturę, występując np. w kryształach. Związane jest to z najmniejszą ilością energii potrzebnej do jego stworzenia. Wiadomo również, że nieperiodyczne układy mogą istnieć w kryształach tylko przez ograniczony czas.
Kafelki Rogera Penrose’a
W latach 70. Roger Penrose matematyk oraz fizyk znany z badań nad czarnymi dziurami odkrył, że możliwe jest utworzenie parkietaża z dwóch różnych kształtów. Parkietaż Penrose’a składa się z dwóch rodzajów płytek: „strzałki” i rombu, układających się w kształt pięcioramiennej gwiazdy.
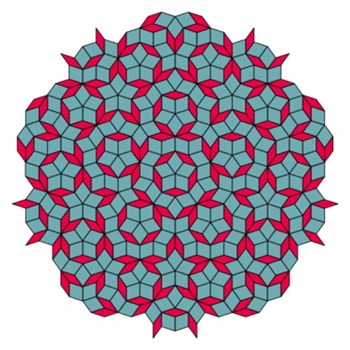
Kafelki Rogera Penrose’a
Powtarzający się wielokrotnie układ, stworzony według zasady, że żadne dwa stykające się kafelki nie mogą tworzyć równoległoboku, udowodnił, że da się utworzyć mozaikę nieperiodyczną, w którym poszczególne elementy w dalszym ciągu nie będą na siebie nachodzić ani nie pozostawią wolnej przestrzeni.
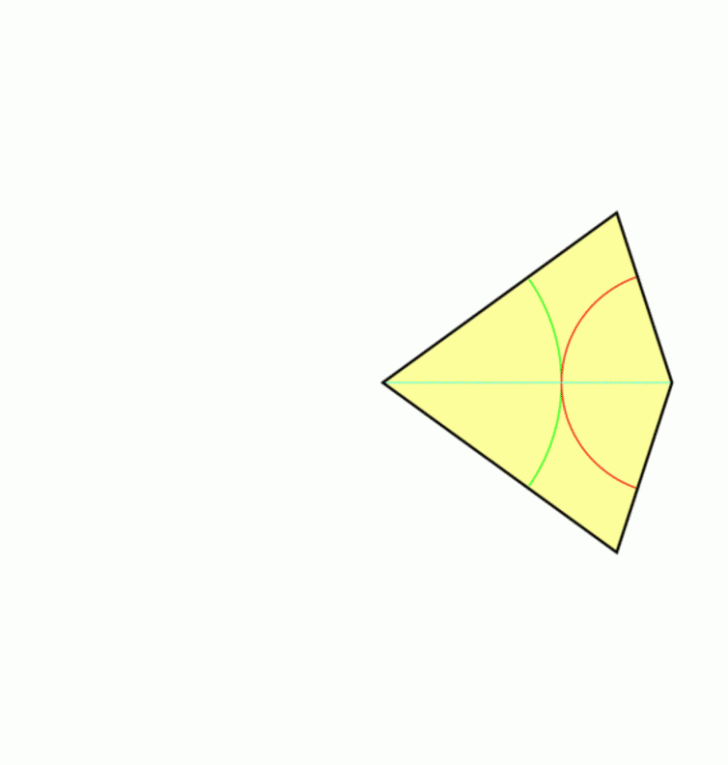
Kafelki Penrose’a. Autor PrzemekMajewski, CC BY-SA
Jeśli przyjrzymy się powstałej w ten sposób kompozycji, zobaczymy, że główny wzór – gwiazda – powtarza się, jednak elementy naokoło niej – czerwone romby układające się w „strzałki” – tworzą za każdym razem inny układ.
Parkietaż Penrose’a jest również przykładem symetrii obrotowej, czyli powtórzeniem dokonanym przez obrót figury wokół punktu o odpowiedni kąt. W tym przypadku jest to dokładnie kąt 72 stopni.
Obracając o pełne 360 stopni, wzór będzie wyglądał tak samo, ale po dowolnym przesunięciu (translacji) fragmenty mozaiki nigdy nie nałożą się na siebie w idealny sposób (przeciwnie do układu periodycznego). Mozaika jest więc przykładem symetrii obrotowej i nietranslacyjnej.
Kwazikryształy
Jeszcze ciekawiej robi się, gdy z dwuwymiarowej płaszczyzny przejdziemy do świata trójwymiarowych obiektów.
W 1984 roku izraelski naukowiec Dan Shechtman obserwując schłodzony stop glinu z magnezem, odkrył strukturę pozornie regularną, jednak w przeciwieństwie do zwykłych kryształów (układów periodycznych) niepowtarzającą się regularnie w przestrzeni.

Kwazikryształ Ho-Mg-Zn w postaci dwunastościanu. Źródło: deltami.edu.pl
Struktura nazwana została kwazikryształem. To, co ją wyróżnia, to fakt, że jest uporządkowanym, ale nieperiodycznym systemem przestrzennym. Kwazikryształy są więc trójwymiarowymi wersjami Kafelek Penrose’a.
Istnienie kwazikryształów było przez wiele lat podawane w wątpliwość, ponieważ wydawało się, że taka struktura byłaby zbyt nietrwała, by istnieć w przyrodzie w stanie stabilnym.

Struktura atomowa kwazikryształu Ag-Al. Źródło: deltami.edu.pl
Shechtman udowodnił, że takie kryształy mogą występować naturalnie w skałach, za co naukowiec otrzymał w 2011 roku Nagrodę Nobla w dziedzinie chemii. Odkrycie postawiło przed światem nauki problem ponownego zdefiniowana, czym są w takim razie kryształy.
A na koniec „wisienka na torcie” nigdy niepowtarzający się w przestrzeni wzór wynika z irracjonalnej liczby znajdującej się w samym sercu struktury.

W regularny pentagon możliwe jest wpisanie pięcioramiennej gwiazdy. Stosunek długości boku gwiazdy, do boku pentagonu, w który zostanie ona wpisana, wynosi 1.618, czyli mniej więcej tyle, co słynna „złota liczba” Phi.